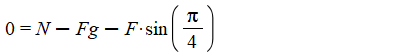Global Reflection of Math Models:
Based on our performance models, the bucket saw will likely slip on a concrete surface before tipping. This is safer than a design that will tip before slipping, since tipping can put the bucket at an unexpected position, which could put the user and others in danger. This is because the bucket saw is circular on its side and the vibration of the jigsaw can create unwanted movements. In addition, a tipped bucket will no longer collect sawdust and make a mess on the floor. ;(
Sliding could potentially be dangerous as well because it would be difficult to cut a piece of wood on a sliding surface and it may bump into an object, which might cause the bucket saw to tip over. According to our math model, slipping will occur at a small force of approximately 4.6 lbs. This is not a realistic force for cutting a piece of wood.
Based on the above arguments, we would need to make further modifications to our product. One possible solution would be to place some weights inside the bucket to increase the stability. However, this would make the bucket saw heavier, thus it would make it less mobile. The second possibility is to add rubber pads on the bottom of the bucket to increase the coefficient of friction between the concrete surface and the bucket saw. The best solution might be to have a combination of the two possible ways of modifying the design. The combination of the two will also increase the tipping force as well as the sliding force, which would also increase the safety of our product.
Math Model 1: Finding Center of Mass
Global Statement:
The goal of this math model is to determine the center of mass of the worktable, the bucket, and the jigsaw combined.
Relevant Physical Dimensions:
The jigsaw is 8 inches long
The jigsaw weighs 3.80 lb.
The bucket weighs 2.00 lb.
The work table and ring together weigh 1.8 lb.
Assumptions:
The bucket has a uniform thickness and density
The blade of the jigsaw aligns with the center of the bucket
Modifications to the bucket have not yet been made
Sketch and Calculations

Reflection and Verification:
To find the center of gravity for each individual part, we had to use different methods. For the bucket, we were able to accurately calculate where the center of gravity is. For the jigsaw, since it is a unique size and shape, we had to estimate the center by doing a balance test. For the balance test, we place the jigsaw on a PVC pipe in both the x and y direction and adjusted the position to where it was most balanced. We used that spot as our center of gravity. For the work table and ring combination, we used the Mass Property Sensor feature of SolidWorks to find the center of gravity.
We found the center of mass of our Bucket Saw to be,
Cgx = 5.76 in. (from the left side of the bucket)
Cgy = 13.625 in. (from the bottom of the bucket)
Therefore, the center of gravity is near the top of the Bucket Saw.
Math Model 2: Finding the Maximum Force Before Tipping
Global Statement:
The goal of this math model is to determine the amount of force a user can push the cutting material on the bucket saw without tipping it.
Relevant Physical Dimensions:
The jigsaw is 8 inches long
The jigsaw weighs 3.80 lb.
The bucket weighs 2.00 lb.
Height of the bucket is 12.875 in.
Diameter of the bucket is 11.520 in.
Assumptions:
The bucket is placed on a perfect surface without slipping
The bucket has not yet been modified
There is no sawdust inside the bucket
The center of mass of the jigsaw is 5.5 inches from the end of the handle in the x-direction and 3.5 inches from the blade base in the y-direction (found using balance on pipe).
The center of mass of the bucket is in the center of the bucket
The user pushes the board at a 45 degree angle with respect to the work table
The block has no mass
The blade aligns with the center of gravity of the jigsaw
The work table has no mass
Sketches:


Basic Diagram for Math Models
FBD for Math Model 2
Solving Equations:
Sum of torque about the origin
Solving for F
Reflection and Verification:
Our model yields a value of approximately 10.60 lbs. as the maximum amount of force that can be applied to the bucked before tipping on a perfect surface without any slipping. The value seems reasonable since the total weight of the bucket and the saw is 7.6 lbs. And our maximum force exceeds the total weight, which is good!
In application, 10.60 lbs. seems to be a small amount of force for the task to be done. We might consider increased support or extra weight into our design to improve the stability of our bucket-saw.


Math Model 3: Finding the Maximum Force Before Slipping
Global Statement:
The goal of this math model is to determine the amount of force a user can push the cutting material on the bucket saw without slipping on a concrete surfaced.
Relevant Physical Dimensions:
The jigsaw weighs 3.80 lb.
The bucket weighs 2.00 lb.
The weight of the work table and the ring combined is 2.00 lb
Assumptions:
The bucket is made of a hard plastic
The bucket is placed on dry concrete
The coefficient of friction between concrete and hard plastic is 0.3
The bucket has not yet been modified
There is no sawdust inside the bucket
The user pushes the board at a 45 degree angle with respect to the work table
The block has no mass
Sketches:


Basic Diagram for Math Models
FBD for Math Model 3
Solving Equations:
Sum of force in the y-direction
Definition of frictional force
Substituting N
Substitute Ff and solve for F
Reflection and Verification:
Our model yields a value of approximately 4.6 lbs. as the maximum amount of force that can be applied to the bucked before slipping on a concrete surface. The value seems reasonable since the total weight of the bucket and the saw is 7.6 lbs. and our maximum force does not exceed the total weight.
In application, 4.6 lbs. seems to be a small amount of force for the task to be done. We might consider increased support or extra weight into our design to improve the stability of our bucket-saw. In addition, we could consider attaching rubber pads on the bottom of the bucket to increase the coefficient of friction to prevent slipping while the device is in use.